Cartesian and polar two-dimensional coordinate systems
This online calculator converts polar coordinates to cartesian coordinates and vice versa.
Cartesian coordinate system on a plane is choosen by choosing the origin (point O) and axis (two ordered lines perpendicular to each other and meeting at origin point).
Thus, any point on a plane can be specified by specifying it's coordinates, which are distance from origin to the perpendicular projections of this point to the axis.
There are other coordinate systems in two-dimensional space, which can be used to find out point location with two numbers. Most commonly used after cartesian is polar coordinate system.
Polar coordinate system on a plane is choosen by choosing the original point (pole) and the ray from the pole called polar axis.
The distance r from any point to pole is called polar radius of point, or radial coordinate, or simply radius. The angle between polar axis and radius is called polar angle, or angular coordinate, or azimuth. Radius and azimuth are polar coordinates of a point.
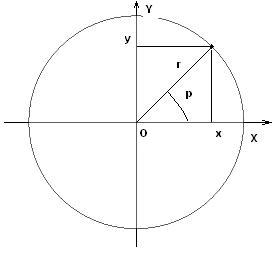
Calculators below convert from polar to cartesian coordinates and vice versa. It is assumed that origin points for both systems are the same and polar axis are directed along positive direction of x-axis.
Conversion from cartesian coordinates to polar coordinates
Conversion from polar coordinates to cartesian coordinates
PLANETCALC, Cartesian and polar two-dimensional coordinate systems
Comments